Ejercicio nº 1.-
a) Efectúa y
simplifica:
![]()
b) Calcula el cociente
y el resto:
![]()
Solución:
![]()
![]()
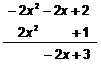
Cociente = 2x - 1
Resto = -2x + 3
Ejercicio nº 2.-
Consideramos el
polinomio P(x) = 7x4 - 2x3 + 3x2 + 1.
a) Halla el cociente y
el resto de la división:
P(x) : (x + 2)
b) ¿Cuánto vale P(-2)?
Solución:
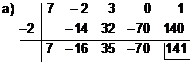
Cociente = 7x3 - 16x2 + 35x - 70
Resto = 141
b) Por el
teorema del resto sabemos que P(-2) = resto, por tanto:
P(-2) = 141.
Ejercicio nº 3.-
Factoriza el siguiente
polinomio:
x4 + 3x3 - 10x2
Solución:
Sacamos
factor común:
![]()
Buscamos las
raíces de x2 + 3x - 10 resolviendo la ecuación:
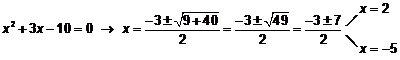
Por tanto:
![]()
Ejercicio nº 4.-
Simplifica la
fracción:
![]()
Solución:
![]()
Ejercicio nº 5.-
Realiza las siguientes
operaciones y simplifica:
![]()
Solución:
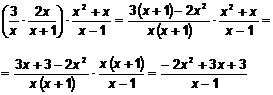
Ejercicio nº 6.-
Resuelve estas ecuaciones:
![]()
Solución:
![]()
![]()
![]()
![]()
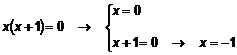
![]()
Cambio: x2 = z ® x4
= z2
z2 21z
100 = 0
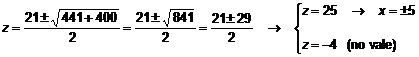
Dos soluciones: x1
= -5, x2 = 5
Ejercicio nº 7.-
Resuelve:
![]()
Solución:
![]()
![]()
![]()
![]()
![]()
Comprobación:
![]()
![]()
Hay una solución: x = -1
![]()
![]()
![]()
![]()
![]()
![]()
Ejercicio nº 8.-
Resuelve esta ecuación:
![]()
Solución:
Factorizamos:
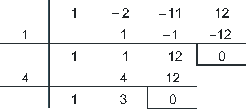
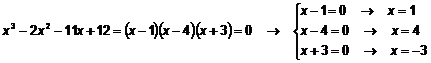
Por tanto, las soluciones de la ecuación son:
![]()
Ejercicio nº 9.-
La raíz cuadrada de la
edad de Marta coincidirá con la que tenga su hija dentro de 2 años. Calcula la
edad de cada una sabiendo que la suma de las edades de ambas es 40.
Solución:
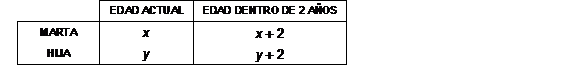
![]()
![]()
® x2
85x + 1 764 = 0
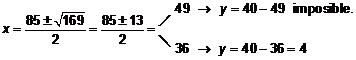
Marta tiene 36 años y su hija 4 años.
Ejercicio nº 10.-
Resuelve
analíticamente el siguiente sistema de ecuaciones e interpreta gráficamente la
solución:
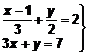
Solución:
Resolvemos analíticamente el sistema:
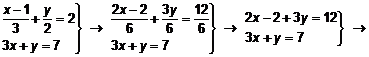
![]()
![]()
![]()
![]()
Solución: x = 1; y = 4
Interpretación gráfica:

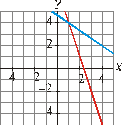
Ejercicio nº 11.-
Resuelve el siguiente sistema:
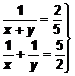
Solución:
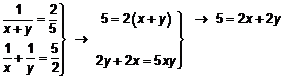
![]()
![]()
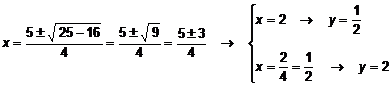
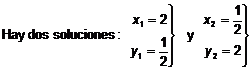
Ejercicio nº 12.-
Un comerciante compró
dos artículos por 30 euros y los vendió por 33,9 euros. En la venta del primer
artículo obtuvo un 10% de beneficio y en la venta del segundo artículo ganó un
15%. ¿Cuánto le costó cada uno de los artículos?
Solución:
Llamamos x al precio del primer artículo e y
al precio del segundo. Así:
![]()
![]()
![]()
![]()
El primer artículo le costó 12 euros y el segundo, 18.
Ejercicio nº 13.-
Resuelve el siguiente sistema de inecuaciones:
![]()
Solución:
![]()
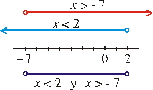
Las soluciones del sistema son las soluciones comunes
a las dos inecuaciones, es decir:
{x < 2 y x
> -7} = {x / -7 < x < 2} = (-7, 2)
Ejercicio nº 14.-
Resuelve:
![]()
Solución:
3x + y ³ 2 es lo mismo
que 3x + y - 2 ³ 0.
![]()
Sustituyendo (2, 1) en la desigualdad 3x + y ³ 2, vemos que la cumple: 3 · 2 + 1 ³ 2.
Además, x £ 2 corresponde a los puntos que se
sitúan a la izquierda de la recta x
= 2 (o sobre ella).
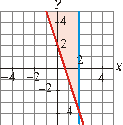
Tomando las soluciones
comunes a las dos desigualdades, llegamos al recinto solución del sistema (la
parte coloreada y las semirrectas que lo limitan):
Ejercicio nº 15.-
Resuelve gráficamente:
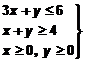
Solución:
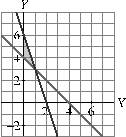
Representamos la recta 3x + y = 6.
![]()
![]()
Si tomamos el punto (0, 0) y lo sustituimos en la
inecuación 3x + y £ 6 vemos que se verifica (3 · 0 + 0 = 0 £ 6).
Luego la solución de ésta inecuación es el semiplano
que contiene a ese punto.
Representamos la recta
x + y = 4.
![]()
En este caso el punto (0, 0) no cumple la
inecuación x + y = ³ 4 (0 4). Por tanto, la solución es el semiplano que no contiene a este punto.
La inecuaciones
x ³ 0, y ³ 0 nos limitan al 1er cuadrante.
La zona sombreada es la solución común al sistema de
inecuaciones.