Ejercicio nº 1.-

Halla el dominio de definición de las funciones:

 

Solución:

 

 

 

Ejercicio nº 2.-

Averigua el dominio de definición de las siguientes funciones, a partir de sus gráficas:

a)                                                                        b)

                                       

 

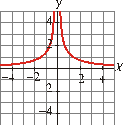
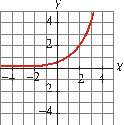
Solución:

b)   Dominio = R

 

Ejercicio nº 3.-

Vamos a considerar todos los rectángulos de 30 cm de perímetro. Si llamamos  x  a la longitud de la base, el área será:

A = (15 - x)

¿Cuál es el dominio de definición de esta función?

 

Solución:

 

 

Ejercicio nº 4.-

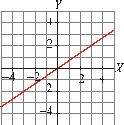
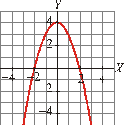
Asocia cada una de estas gráficas con su correspondiente ecuación:

I)                                                                                   II)

                                                

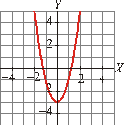
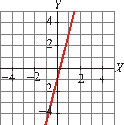
III)                                                                                  IV)

                                                

 

Solución:

a)  III          b)  I          c)  II          d)  IV

 

 

Ejercicio nº 5.-

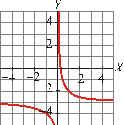
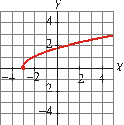
Asocia cada gráfica con su correspondiente ecuación:

I)                                                                                   II)

                                                

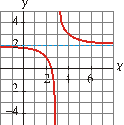
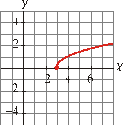
III)                                                                                  IV)

                                                

 

Solución:

a)  III                b)  II                 c)  I                  d)  IV

 

 

Ejercicio nº 6.-

 

Solución:

Escribimos la ecuación punto-pendiente:

Operando:

 

 

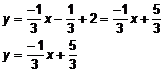
Ejercicio nº 7.-

Sabiendo que 15° C (grados centígrados) equivalen a 59° F (grados Fahrenheit), y que
30° C son 86° F, averigua cuántos grados centígrados son 70° F. ¿Y 92° F?

 

Solución:

Vamos a resolver el problema mediante una interpolación lineal.

Por tanto:

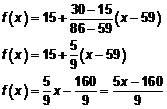
Así:

f (92) = 33,33

70° F equivalen a 21,11° C, y 92° F, a 33,33° C.

 

 

Ejercicio nº 8.-

Representa gráficamente la siguiente función:

 

Solución:

•  El vértice de la parábola es:

  

•  Puntos de corte con los ejes:

  

  

•  Hallamos algún otro punto:

 

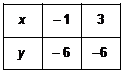
•  La gráfica es:

 

 

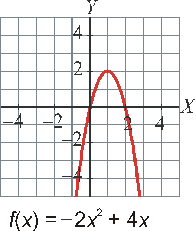
Ejercicio nº 9.-

Representa la siguiente función:

 

Solución:

Si x < -1, tenemos un trozo de parábola.

Si x ≥ -1, tenemos un trozo de recta.

La gráfica es:

 

 

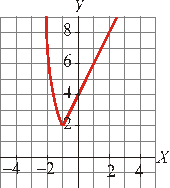
Ejercicio nº 10.-

siguiente:

                                            

 

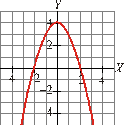
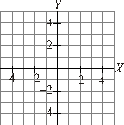
Solución:

 

 

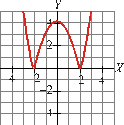
Ejercicio nº 11.-

Ponemos al fuego un cazo con hielo cuya temperatura es de -20° C. En 10 minutos se descongela y se mantiene a 0° C otros 10 minutos más. Un cuarto de hora más tarde llega a alcanzar 100° C.

a)  Representa la función que describe este fenómeno y halla su expresión analítica.

b)  ¿Cuál es el dominio y el recorrido de la función?

 

Solución:

a)  Llamamos  x = Tiempo (minutos)

                        y = Temperatura (° C)

  1.er tramo:  Recta que pasa por  (0, -20)  y  (10, 0).

n = -20  por cortar al eje  Y  en  (0, -20).

Ecuación:  y = 2x - 20

  2. ° tramo:  Función constante constante  y = 0

  3. er tramo:  Recta que pasa por  (20, 0)  y  (32, 100).

 

 

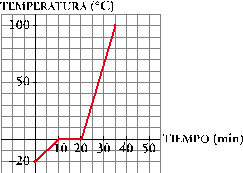
La expresión analítica será:

 

 

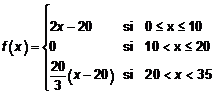
b)  Dominio = [0, 35]                          Recorrido = [-20, 100]