1. En un determinado momento un avión se encuentra situado con respecto a dos puntos como muestra la figura:
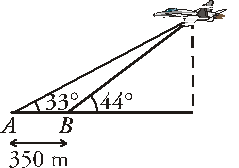
Halla
las distancias del avión a los puntos
A
y B, así como la altura a la que se encuentra en
dicho instante.
Solución:
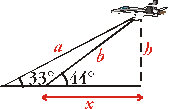
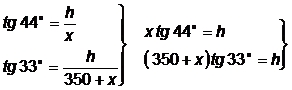
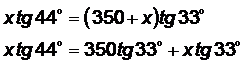
![]()
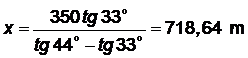
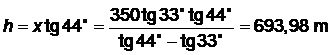
El avión se encuentra a 693,98 m de altura.
Por
otra parte:
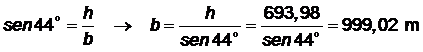
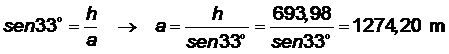
El
avión está a 1274,20 metros de
A y a
999,02 metros de B.
2.
Calcula
los lados y los ángulos del siguiente triángulo:
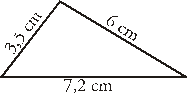
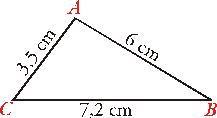
Solución:
Como
conocemos los tres lados
(y cada lado es menor que la suma
de los otros dos),
existe
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Por
tanto:
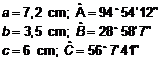
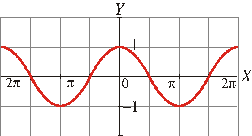
3. a) Dado la siguiente gráfica,
escribe la ecuación de la función correspondiente:
b) Representa la siguiente función
en los ejes que se dan:
y = cos 2x
Solución:
a) La gráfica corresponde a la función y = cos x.
b) Hacemos una tabla de valores:
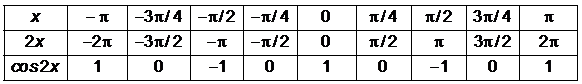
La
gráfica sería:
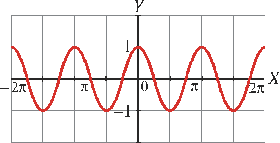
4.
Demuestra
que:
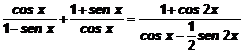
Solución:
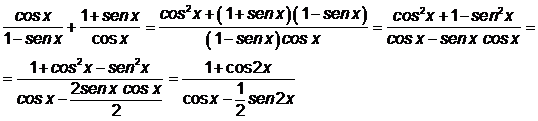
5.
Resuelve
la ecuación trigonométrica:
Solución:
![]()
![]()
![]()
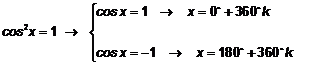
![]()
6.
Halla
en forma binómica y representa la solución obtenida:
![]()
Solución:
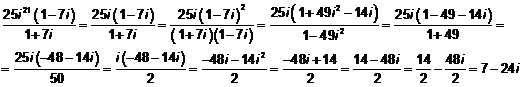
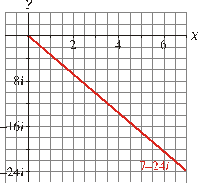
Representación
gráfica:
7.
Halla
todas las soluciones de la ecuación:
2z6 + 2 = 0
Solución:
![]()
![]()
Las
seis soluciones son:
![]()
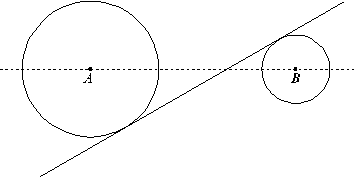
8. Los
radios de las circunferencias de la figura son tales que uno es el doble del
otro. El ángulo que forma la tangente a las circunferencias con la línea que
une sus centros es de 30°. Calcula los radios de las
circunferencias sabiendo que la distancia entre sus centros es de 18 cm.
Solución:
Llamamos x
e y a los
radios de las circunferencias.

![]()
![]()
Resolvemos
el sistema formado por:
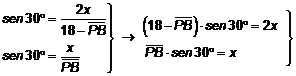
![]()
![]()
x = 6 · sen 30° = 3 ® 2x = 6 cm.
Los
radios de las circunferencias miden 3 cm y 6 cm.