Ejercicio nº 1.-
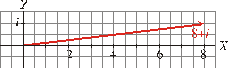
Calcula y representa gráficamente la
solución:
![]()
Solución:
![]()
![]()
Representación gráfica:
Ejercicio nº 2.-
![]()
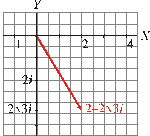
a) Represéntalo gráficamente y escribe su opuesto y su conjugado.
b) Expresa z
en forma polar.
Solución:
a)
![]()
![]()
![]()
![]()
![]()
Ejercicio nº 3.-
Halla el módulo y el argumento de
![]()
Solución:
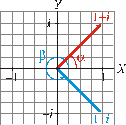
Expresamos
1 - i
y 1 + i en
forma polar:
![]()
![]()
![]()
![]()
Por tanto:
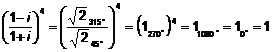
Módulo = 1 y Argumento = 0°.
Ejercicio nº 4.-
Halla las raíces sextas de -1 e interpreta gráficamente los resultados
obtenidos.
Solución:
![]()
Las seis raíces son:
![]()
Interpretación gráfica:

Los afijos de las seis raíces ocupan los
vértices de un hexágono regular centrado en el origen.
Ejercicio nº 5.-
Resuelve la ecuación:
![]()
Solución:
![]()
![]()
![]()
Ejercicio nº 6.-
Busca una ecuación de segundo grado cuyas
soluciones sean un número complejo z
y su conjugado.
Solución:
![]()
![]()
![]()
![]()
![]()
Por tanto, la ecuación de segundo grado que
cumple las condiciones es z2 - 2az + a2 + b2 = 0, siendo a
y b
números reales cualesquiera.