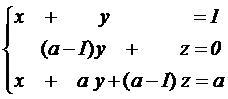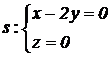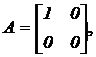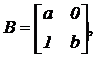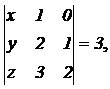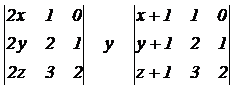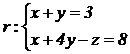Página de inicio.

Matemáticas II Julio 2018

BAREMO DEL EXAMEN: Se elegirá sólo UNA de las dos OPCIONES, A o B, y se han de hacer los tres problemas de esa opción.

Cada problema se puntuará hasta 10 puntos.

La calificación del ejercicio será la suma de las calificaciones de cada problema dividida entre 3 y aproximada a las centésimas.

Se permite el uso de calculadoras siempre que no sean gráficas o programables, y que no puedan realizar cálculo simbólico ni almacenar texto o fórmulas en memoria. Se utilice o no la calculadora, los resultados analíticos, numéricos y gráficos deberán estar siempre debidamente justificados.

OPCIÓN A

PROBLEMA A.1. Dado el sistema de ecuaciones

donde a es un parámetro real. Se pide obtener razonadamente, escribiendo todos los pasos del razonamiento utilizado:

a) Los valores del parámetro a para los cuales el sistema es compatible. (5 puntos)

b) Las soluciones del sistema cuando a = 1. (3 puntos)

c) Las soluciones del sistema cuando a = 0. (4 puntos)

Solución

PROBLEMA A.2. Se tienen el plano p: x – y + z – 3 = 0, la recta

y el punto

A = (1, 1, 1). Obtener razonadamente, escribiendo todos los pasos del razonamiento utilizado:

a) La recta que pasa por A, corta a la recta s y es paralela al plano π. (4 puntos)

b) El plano que pasa por A, es perpendicular al plano π y paralelo a la recta s. (3 puntos)

c) Discute si el punto (3,2,1) está en la recta paralela a s que pasa por (5,3,1). (3 puntos)

Solución

PROBLEMA A.3. Consideramos la función f(x) = a x³ + b x² + c x cos ( p x ), que depende de los parámetros a, b, c. Obtener razonadamente, escribiendo todos los pasos del razonamiento utilizado:

a) La relación entre los coeficientes a, b, c sabiendo que f(x) toma el valor 22 cuando x = 1. (2 puntos)

b) La relación que deben verificar los coeficientes a, b y c para que sea horizontal la recta tangente a la curva y = f(x) en el punto P de dicha curva, sabiendo que la abscisa del punto P es x = 1. (4 puntos)

c) (4 puntos)

Solución

OPCIÓN B

PROBLEMA B.1. Resolver los siguientes apartados, escribiendo todos los pasos del razonamiento utilizado:

a) Dadas A y B, matrices cuadradas del mismo orden tales que A B = A y B A = B, deducir que A² = A y B² = B. (4 puntos)

b) Dada la matriz

se pide encontrar los parámetros a, b para que la matriz

cumpla que B^2 = B pero A B ¹ A y B A ¹ B (2 puntos)

c) Sabiendo que

Obtener razonadamente el valor de los determinantes

(4 puntos)

Solución

PROBLEMA B.2. Dada la recta

, se pide obtener razonadamente,

escribiendo todos los pasos del razonamiento utilizado:

a) Las ecuaciones paramétricas de la recta r (3 puntos)

b) La ecuación del plano p que es paralelo a r y pasa por los puntos (5,0,1) y (4,1,0) (4 puntos)

c) La distancia entre la recta r y el plano p obtenido en el apartado anterior. (2 puntos)

Solución

PROBLEMA B.3. Dentro de una cartulina rectangular se desea hacer un dibujo que ocupe un rectángulo R de 600 cm² de área de manera que:

Por encima y por debajo de R deben quedar unos márgenes de 3 cm de altura cada uno. Los márgenes a izquierda y derecha de R deben tener una anchura de 2 cm cada uno.

Obtener razonadamente, escribiendo todos los pasos del razonamiento utilizado:

a) El área de la cartulina en función de la base x del rectángulo R. (3 puntos)

b) El valor de x para el cual el área de la cartulina es mínima. (5 puntos)

c) Las dimensiones de dicha cartulina de área mínima. (3 puntos)

Solución

Página de inicio.