Página de inicio.

Matemáticas II Julio 2022

BAREMO DEL EXAMEN: El alumno elegiré solo TRES problemas entre los seis propuestos.

Cada problema se puntuará hasta 10 puntos.

La calificación del ejercicio será la suma de las calificaciones de cada problema dividida entre 3 y aproximada a las centésimas.

Se permite el uso de calculadoras siempre que no sean gráficas o programables, y que no puedan realizar cálculo simbólico ni almacenar texto o fórmulas en memoria. Se utilice o no la calculadora, los resultados analíticos, numéricos y gráficos deberán estar siempre debidamente justificados.

En las respuestas se deben escribir todos los pasos del razonamiento utilizado.

Problema 1. Dado el sistema de ecuaciones

.

a) Discutir el sistema en función del parámetro real a. (5 puntos)

b) Encontrar todas las soluciones del sistema cuando este sea compatible. (5 puntos)

Solución

Problema 2. Dada la matriz

a) Calcular los valores de los parámetros a y b para que se cumpla.

.

(4 puntos)

b) Para los valores a y b obtenidos en el apartado anterior, calcular A³ y A⁴. (3 puntos)

c) Calcular det (A ^-50) cuando a ² – b ² ¹ 0 (3 puntos)

Solución

Problema 3. Dados los puntos A = ( 2, 0, 0 ) y B = ( 0, 1, 0 ), y la recta

a) Hallar la ecuación de la recta r que pasa por los puntos A y B. (2 puntos)

b) Determinar la ecuación implícita del plano que contiene a la recta s y es paralelo a la recta r. (4 puntos)

c) Calcular la distancia del punto A a la recta s. (4 puntos)

Solución

Problema 4. Dados los puntos A = ( 2 , 1, – 2 ) y B = ( 3, 2, 3 ), y el plano p definido por 2 x + 2 y + z = 3, obtener:

a) El punto de corte C entre el plano π y la recta perpendicular a π que pasa por B.
(5 puntos)

b) El área del triángulo cuyos vértices son A, B y C . (5 puntos)

Solución

Problema 5.

a) Calcular indicando todos los pasos, la siguiente integral indefinida: (5 puntos)

b) Determinar, en función de t, el valor

(2 puntos)

c) Determinar el valor de t mayor que 8 para que			sea igual a
	(2 puntos)

Solución

Problema 6. Considerar la función

para los valores positivos de x. Por cada

punto M = ( x, f(x) ) de la gráfica de f se trazan dos rectas paralelas a los ejes coordenados, OX y OY. Estas dos rectas, junto con los ejes de coordenadas, definen un rectángulo.

Obtener razonadamente, escribiendo todos los pasos del razonamiento utilizado:

a) Determinar el área del rectángulo en función de x. (3 puntos)

b) Encontrar el punto M que proporciona mayor área y calcular esta área. (7 puntos)

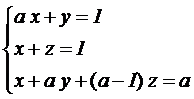
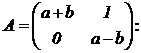
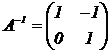Solución

Página de inicio.