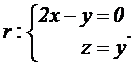Matemáticas II Julio
2025 Reserva
BAREMO DEL EXAMEN: Cada
problema se puntuará hasta 2,5 puntos.
La calificación del
ejercicio será la suma de las calificaciones de cada problema.
Se permite el uso de
calculadoras siempre que no sean gráficas o programables, y que no puedan
realizar cálculos simbólicos ni almacenar texto o fórmulas en memoria. Se
utilice o no la calculadora, los resultados analíticos, numéricos y gráficos
deberán estar siempre debidamente justificados.
A partir de la
tercera falta de ortografía se deducirán -0,10 puntos hasta un máximo de un
punto.
Por errores en la
redacción, en la presentación, falta de coherencia, falta de cohesión,
incorrección léxica e incorrección gramatical se podrá deducir un máximo de
medio punto.
En las
respuestas se deben escribir todos los pasos del razonamiento utilizado.
PREGUNTA 1: PROBABILIDAD
Y ESTADÍSTICA (2,5 puntos)
Se ha realizado una
encuesta a 120 miembros de un club de lectura sobre sus preferencias
literarias. La siguiente tabla muestra los resultados clasificados por edad y
tipo de obra preferido.
|
Edad/Tipo de obra |
Novela |
Poesía |
Obras
de teatro |
Ensayos |
|
< 25 años |
17 |
6 |
7 |
1 |
|
25 – 60 años |
22 |
17 |
10 |
3 |
|
> 60 años |
8 |
12 |
11 |
6 |
1.1 (0.75 puntos) ¿Cuál es la
probabilidad de que el tipo de obra preferido de una persona seleccionada al
azar no sea el ensayo?
1.2 (0.75 puntos) Si se sabe que un
miembro del club NO tiene como tipo de obra preferido la poesía, ¿cuál es la
probabilidad de que tenga 25 años o más?
1.3 (1
punto) Dados 10 miembros del club que tienen entre 25 y 60 años, ambos
incluidos. ¿Cuál es la probabilidad de que como mucho 3 de ellos tengan como
tipo de obra preferido o bien las obras de teatro o bien los ensayos?
PREGUNTA 2: ÁLGEBRA (2,5 puntos)
Responda al apartado 2.1 o al apartado 2.2
2.1 Dadas las
matrices
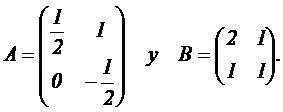
Calcular:
2.1.1 (0.75 puntos) La matriz X, si existe, tal que 2 A X = B X + I, siendo I la matriz identidad
2 x 2.
2.1.2 (0.75 puntos)
Si existen, los valores del parámetro real
a tales que 4 A2
+ a A – I = 0, siendo 0 la matriz nula
2 x 2.
2.1.3 (1 punto) A12.
___________________________________________________________________
2.2 Sea el sistema de ecuaciones lineales
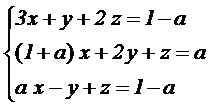
donde a es un parámetro real. Se pide:
2.2.1
(1.25 puntos) Discutir el sistema en
función del parámetro a.
2.2.2
(1.25 puntos) Calcular las soluciones del sistema cuando este sea compatible.
PREGUNTA 3: GEOMETRÍA (2,5 puntos)
Responda al apartado 3.1 o al apartado 3.2
3.1 Dados el plano
p: 2 x – z = 1, calcular:
|
3.1.1 (1.25 puntos) Si existe, el plano
perpendicular a p que contiene
a la recta |
|
3.1.2 (1.25 puntos)
Los planos paralelos a p cuya distancia
la punto P = (0,1,2) es 2.
___________________________________________________________________
3.2 Se considera
el plano p con
ecuación
2 x +3 y – z = 0 y los
cuatro puntos A = (0,0,0), B = (10,0, –20), C = (0,15, –30) y D = (1,2, –1).
3.2.1 (0.5 puntos) Comprobar si el
triángulo ABC pertenece al plano p.
3.2.2
(0.5 puntos) Calcular la distancia del punto D al plano π.
3.2.3
(1.5 puntos) Calcular las coordenadas de la proyección del
punto D sobre el
plano formado por los
puntos A, B y C.
PREGUNTA 4: ANÁLISIS (2,5 puntos)
Responda al apartado 4.1 o al apartado 4.2
4.1 Sea la
función real de variable real
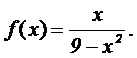
4.1.1
(0.75 puntos) Calcular el dominio
de definición, las asíntotas y los intervalos de crecimiento y decrecimiento de
la función f.
4.1.2
(0.25 puntos) Dibujar la curva y =
f(x).
4.1.3 (0.75 puntos) Hallar todas las primitivas de
f.
4.1.4 (0.75 puntos) Calcular el área comprendida entre las curvas y =
f(x), x = – 1 , x = 1 y el eje de
abcisas.
___________________________________________________________________
4.2 Se
quiere construir un bote de refresco cilíndrico de volumen 33 cm3 que tenga un área total (incluyendo las
tapas) mínima. Se pide:
4.2.1
(0.5 puntos) Expresar el área
total del bote en función del radio de su base y de su altura.
4.2.2 (1.5 puntos) Obtener
las dimensiones que minimizan el área total del bote.
4.2.3 (0.5 puntos) Hallar
dicha área.