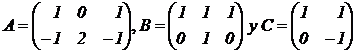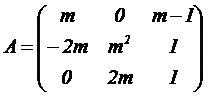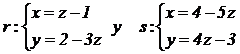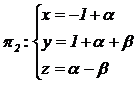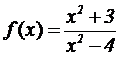Matemáticas II Junio
2022
BAREMO DEL EXAMEN: El alumno elegiré
solo TRES problemas entre los seis propuestos.
Cada problema se puntuará hasta 10
puntos.
La calificación del ejercicio será
la suma de las calificaciones de cada problema dividida entre 3 y aproximada a
las centésimas.
Se permite el uso de calculadoras siempre
que no sean gráficas o programables, y que no puedan realizar cálculo simbólico
ni almacenar texto o fórmulas en memoria. Se utilice o no la calculadora, los
resultados analíticos, numéricos y gráficos deberán estar siempre debidamente
justificados.
En las respuestas se deben escribir
todos los pasos del razonamiento utilizado.
|
Problema 1.
Dadas las matrices |
|
. Se pide |
a)
Demostrar que C – A BT tiene inversa y
calcularla. (4 puntos)
b) Calcular la matriz
X que verifica
C X = A BT X + I,
donde I es la matriz identidad. (3 puntos)
c)
Justificar que ( A BT )n = 2n
I para todo número natural n.
(3 puntos)
|
Problema 2.
Dada la matriza |
|
. Determinar: |
a)
El rango de la matriz
A en función del parámetro real m. (4
puntos)
b) La matriz inversa de
A en el caso
m = 2. (4
puntos)
c)
El número real m
para el cual el determinante de la matriz 2A es
igual a –8. (2 puntos)
|
Problema 3.
Dadas las rectas |
|
. |
a)
Indicar
justificadamente la posición relativa de
las rectas r y s. (5
puntos)
b)
Hallar la
ecuación de la recta l
que pasa por el origen y corta a r y s.
(5 puntos)
|
Problema 4.
Dados los planos p1: 2 x – y –
z + 4 = 0 y |
|
y la recta |
|
|
|
|
a)
Calcular la posición relativa de p1 y p2. (3 puntos)
b)
Calcular el punto
P´ que es el simétrico al punto P =
(1,0,0) respecto del plano p1. (4 puntos)
c)
Calcular, si existe, el punto de intersección de p1 y r. (3
puntos)
|
Problema 5.
Consideremos la función |
|
. Obtener: |
a)
El dominio y los puntos de corte con los ejes. (1 punto)
b) Las asíntotas de la función. (2
puntos)
c)
Los intervalos de crecimiento y decrecimiento, y los
extremos. (3 puntos)
d) La integral de la función f(x). (4
puntos)
Problema 6. Se desea construir un cuadrado y un triángulo
equilátero cortando en dos partes un cable de acero de 240 m. de longitud.
a)
Calcular la suma
de las áreas del triángulo y del cuadrado en función del valor x que corresponde con los metros que mide un
lado del triángulo. (3 puntos)
b)
Calcular la longitud
de cable necesaria para construir el triángulo de modo que la suma de las áreas
del triángulo y del cuadrado sea mínima y calcular el área mínima. (7 puntos)