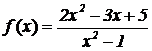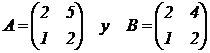Matemáticas aplicadas a las
Ciencias Sociales II Julio 2020
BAREMO
DEL EXAMEN:
Se
han de contestar tres problemas de entre los seis propuestos.
Cada problema se valorará de
Se permite el uso de calculadoras siempre
que no sean gráficas o programables, y que no puedan realizar cálculo simbólico
ni almacenar texto o fórmulas en memoria. Se utilice o no la calculadora, los
resultados analíticos, numéricos y gráficos deberán estar siempre debidamente
justificados. Está permitido el uso de regla. Las gráficas se harán con el
mismo color que el resto del examen.
Todas las respuestas han de estar debidamente
razonadas.
Problema 1. Para fertilizar
una parcela de cultivo se utilizan dos tipos de fertilizantes, A y B. El
cultivo de la parcela necesita un mínimo de 120 kilos de nitrógeno y 110 kilos
de fósforo. El fertilizante A contiene un 25% de nitrógeno y un 15% de fósforo,
siendo su precio de 1,2 euros el kilo, mientras que el fertilizante B contiene
un 16% de nitrógeno y un 40% de fósforo y cuesta 1,6 euros el kilo.
a)
¿Qué cantidad se
necesita de cada tipo de fertilizante para que el coste de la fertilización
resulte mínimo? (8 puntos)
b)
¿Cuál es ese coste
mínimo? (2 puntos)
|
Problema 2.
Dada la función |
|
, se pide: |
a)
Su dominio y los puntos
de corte con los ejes coordenados. (2 puntos)
b)
Las asíntotas
horizontales y verticales, si existen. (2 puntos)
c)
Los intervalos de
crecimiento y decrecimiento. (2 puntos)
d)
Los máximos y
mínimos locales. (2 puntos)
e)
La representación
gráfica de la función a partir de los resultados de los apartados anteriores. (2
puntos)
Problema 3. Si un habitante de la
ciudad de Megalópolis es portador del anticuerpo A, entonces 2 veces de cada 5
es portador del anticuerpo B. Por el contrario, si no es portador del
anticuerpo A, entonces 4 veces de cada 5 no es portador del anticuerpo B. Si
sabemos que la mitad de la población es portadora del anticuerpo A, calcula:
a)
La probabilidad
de que un habitante de Megalópolis
sea portador del anticuerpo B.
b)
La probabilidad
de que si un habitante de Megalópolis
es portador del anticuerpo B lo sea también del anticuerpo A.
c)
La probabilidad de que si un habitante de
Megalópolis no es portador del
anticuerpo B, tampoco lo sea del anticuerpo A.
d) La probabilidad de que un habitante de Megalópolis sea portador del anticuerpo A y no lo sea del anticuerpo B.
(Cada apartado puntúa 2´5 puntos)
|
Problema 4.
Dada las matrices |
|
, se pide: |
a)
Halla la matriz
inversa de A. (3 puntos)
b)
Explica porque la
matriz B no
tiene inversa. (2 puntos)
c)
Razona porque la
matriz A B no
tiene inversa. (2 puntos)
d) Resuelve la ecuación matricial A B – A X = B A. (3 puntos)
Problema 5. Una
empresa farmacéutica lanza al mercado un nuevo fármaco que se distribuye en
cajas de seis unidades. La relación entre el precio de cada caja y el beneficio
mensual obtenido en euros viene dada por la función
B(x) = – x2 +16 x – 55,
donde x es el precio
de venta de una caja. Se pide:
a)
¿Qué beneficio
obtiene cuando vende cada caja a 6 euros? (2 puntos)
b)
¿Entre qué valores
debe fijar el precio de venta de cada caja para obtener beneficios? (2
puntos)
c)
Calcula a qué
precio ha de vender cada caja para que el beneficio sea máximo. ¿Cuál es el
beneficio máximo? (2+1 puntos)
d)
¿Entre qué
valores el beneficio crece y entre qué valores el beneficio decrece? (3
puntos)
Problema 6. Un
profesor evalúa a sus estudiantes a través de un trabajo final. El profesor
sabe por experiencia que el 5% de los trabajos no son originales, sino que son
plagios. El profesor dispone de un programa informático para detectar plagios.
La probabilidad de que el programa no clasifique correctamente un trabajo
plagiado es 0,04 y la probabilidad de que clasifique como plagio un trabajo
original es 0,02.
a)
Calcula la
probabilidad de que un trabajo final, elegido al azar, sea clasificado como
plagio por el programa informático. (3
puntos)
b)
Un trabajo es
inspeccionado por el programa informático y es clasificado como original. ¿Cuál
es la probabilidad de que dicho trabajo sea un plagio? (4 puntos)
c)
¿Qué porcentaje
de trabajos finales son plagios y a la vez son clasificados como tales por el
programa? (3 puntos)