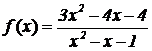Matemáticas aplicadas a las
Ciencias Sociales II Julio 2022
BAREMO
DEL EXAMEN:
Se
han de contestar tres problemas de entre los seis propuestos.
Cada problema se valorará de
Se permite el uso de calculadoras siempre
que no sean gráficas o programables, y que no puedan realizar cálculo simbólico
ni almacenar texto o fórmulas en memoria. Se utilice o no la calculadora, los
resultados analíticos, numéricos y gráficos deberán estar siempre debidamente
justificados. Está permitido el uso de regla. Las gráficas se harán con el
mismo color que el resto del examen.
Todas las respuestas han de estar debidamente
razonadas.
|
Problema 1.
Consideramos las matrices |
|
a)
Justifica cuales
de las siguientes operaciones se pueden realizar y efectúa las que sean
realizables.
a.1) B + 2CA (1 punto)
a.2) A – (BC)T,
siendo (BC)T la matriz
traspuesta de BC. (2
puntos)
a.3) CAB (2 puntos)
b)
Resuelve la
ecuación matricial
![]() ,
,
siendo CT la matriz traspuestas de C. (5 puntos)
Problema 2. Un vendedor dispone de café colombiano y café brasileño, y
con ellos realiza mezclas que pone a la venta. Si mezcla a partes iguales los
dos tipos de café, obtiene una mezcla que vende a 15 euros el kilo; si la
proporción en la mezcla es de una parte de café colombiano por tres partes de
café brasileño, vende la mezcla resultante a 10 euros el kilo. El vendedor
dispone de 100 kilos de café colombiano y de 210 kilos de café brasileño. Desea
hacer las dos mezclas de modo que sus ingresos por venta sean máximos.
a)
Halla cuántos
kilos de cada mezcla debe producir para obtener el ingreso máximo.
(8 puntos)
b)
¿Cuál es dicho ingreso
máximo? (2 puntos)
|
Problema 3.
Se considera la función |
|
. Se pide: |
a)
Su dominio y los
puntos de corte con los ejes coordenados. (2
puntos)
b)
Las asíntotas
horizontales y verticales, si existen. (2
puntos)
c)
Los intervalos de
crecimiento y decrecimiento. (2 puntos)
d)
Los máximos y
mínimos locales, si existen. (2 puntos)
e)
La representación
gráfica de la función a partir de los resultados anteriores. (2
puntos)
Problema 4. Una
máquina está productiva durante un año desde su compra. Se sabe que el
rendimiento (en porcentaje) que tiene la máquina meses después de su compra
viene dado por la función
![]()
para cualquier x
entre 0 y 12.
a)
¿Es el
rendimiento que tiene la máquina un mes después de su compra superior al
rendimiento que tiene dos meses después de su compra? (2 puntos)
b)
¿Tras cuántos
meses después de su compra alcanza la máquina su mayor rendimiento?; ¿cuál es
dicho rendimiento máximo? (4 puntos)
c)
A lo largo del
año, ¿tiene en algún momento la máquina un rendimiento inferior al 10%? (4 puntos)
Problema 5. Dados dos sucesos A y B, se sabe que P(B) = 0,4, P(AcÇBc) = 0,2 y
P(AÇB)) = 0,3, siendo Ac y Bc los sucesos
complementarios de A y B , respectivamente. Se pide:
a)
Calcula la
probabilidad del suceso AÈB. (2´5
puntos)
b)
Calcula la
probabilidad de que solamente se verifique uno de los sucesos. (2´5
puntos)
c)
Calcula la
probabilidad de B condicionado a A. (2´5
puntos)
d) ¿Son independientes los sucesos A y B? (2´5 puntos)
Problema 6. El
director de una entidad que audita la contabilidad de empresas sabe, por
experiencias pasadas, que cuando se hace una auditoría el 30% de las empresas
merece una calificación de «Excelente», el 50% de las empresas merece la
calificación de «Aceptable» y el 20% restante merece una calificación de
«Deficiente». El director también sabe que entre los auditores de su entidad
hay un 90% de auditores que siempre auditan correctamente y dan a cada empresa
la calificación que merece; pero hay un 10% de auditores que no auditan
correctamente y dan siempre una calificación de «Aceptable».
a)
¿Qué
proporción de empresas auditadas por esa entidad recibe la calificación de
«Deficiente»? (3 puntos)
b)
¿Qué proporción
de empresas auditadas por esa entidad recibe la calificación que realmente
merece? (3
puntos)
c)
Para analizar si un determinado auditor audita
correctamente o no, el director le encarga que audite la contabilidad de una
empresa escogida al azar. No sabemos cuál es la calificación que merece esa
empresa. Si el auditor da la calificación de «Aceptable», ¿cuál es la
probabilidad de que este auditor sea uno de los que siempre auditan
correctamente? (4
puntos)
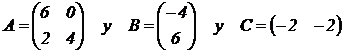 .
.