Matemáticas II Julio
2015
BAREMO DEL EXAMEN: Se elegirá sólo
UNA de las dos OPCIONES, A o B, y se han de hacer los tres problemas de esa
opción.
Cada problema se puntuará hasta 10
puntos.
La calificación del ejercicio será
la suma de las calificaciones de cada problema dividida entre 3 y aproximada a
las centésimas.
Se permite el uso de calculadoras siempre
que no sean gráficas o programables, y que no puedan realizar cálculo simbólico
ni almacenar texto o fórmulas en memoria. Se utilice o no la calculadora, los
resultados analíticos, numéricos y gráficos deberán estar siempre debidamente
justificados.
OPCIÓN A
|
PROBLEMA A.1.
Dado el sistema de ecuaciones |
|
donde a es un |
parámetro
real. Obtener razonadamente, escribiendo
todos los pasos del razonamiento utilizado:
a)
La solución del sistema cuando a = – 1. (3 puntos)
b) Todas las soluciones del sistema cuando a = 0. (3 puntos)
c)
El valor de a para el que
el sistema es incompatible. (4 puntos)
|
PROBLEMA A.2.
Se dan las rectas |
|
y el punto P ( 0 , 3, – 2 ). |
Obtener
razonadamente, escribiendo
todos los pasos del razonamiento utilizado:
a)
Las ecuaciones de la recta que pasa por el punto P y es paralela a la recta r. (3
puntos)
b) La ecuación del plano que contiene a la recta r y es paralelo a la recta s. (4
puntos)
c)
La distancia entre las rectas r y s.
(3 puntos)
|
PROBLEMA A.3.
Se da la función f definida por |
|
Obtener
razonadamente, escribiendo
todos los pasos del razonamiento utilizado:
a)
El dominio y las asíntotas de la función f. (3
puntos)
b) Los intervalos de crecimiento y decrecimiento de la
función f. (4 puntos)
|
c) |
La integral |
|
(3
puntos) |
OPCIÓN B
|
PROBLEMA B.1.
Se dan las matrices |
|
|
Obtener
razonadamente, escribiendo todos los pasos del
razonamiento utilizado:
a)
Los valores
de x para los que la matriz B tiene inversa. (3
puntos)
|
b) |
El valor del determinante
de las matrices A3 y |
|
sabiendo que el valor |
del
determinante de la matriz A es
8.
(4 puntos)
|
c) |
Los valores de x,
y, z para los cuales |
|
(3
puntos) |
|
PROBLEMA B.2.
Se dan las rectas |
|
y el plano |
π: 2 x + m z + 1 = 0, siendo m un
parámetro real. Obtener razonadamente,
escribiendo todos los pasos del razonamiento utilizado:
a)
La posición
relativa de las rectas r y s
y el punto (o puntos) comunes a r
y s.
(4 puntos)
b)
El valor del
parámetro m para que la recta s sea paralela al plano π. (3
puntos)
c)
La ecuación del
plano que contiene a la recta s y al punto P
( 1 , 2, 4 ). (3 puntos)
PROBLEMA B.3. Se va a
construir un depósito de
Obtener
razonadamente, escribiendo
todos los pasos del razonamiento utilizado:
a)
El coste total
del depósito en función de la longitud x
de un lado de la base. (3 puntos)
b)
Las longitudes
del lado de la base y de la altura del depósito para que dicho coste total sea
mínimo. (5 puntos)
c)
El valor del
mínimo coste total del depósito. (2 puntos)
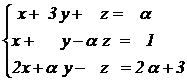 ,
,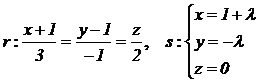
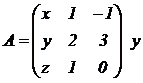
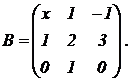
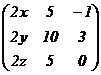 ,
,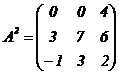 .
.