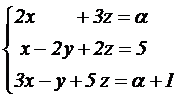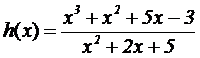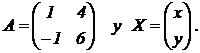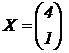Matemáticas II Julio
2019
BAREMO DEL EXAMEN: Se elegirá sólo
UNA de las dos OPCIONES, A o B, y se han de hacer los tres problemas de esa
opción.
Cada problema se puntuará hasta 10
puntos.
La calificación del ejercicio será
la suma de las calificaciones de cada problema dividida entre 3 y aproximada a
las centésimas.
Se permite el uso de calculadoras siempre
que no sean gráficas o programables, y que no puedan realizar cálculo simbólico
ni almacenar texto o fórmulas en memoria. Se utilice o no la calculadora, los
resultados analíticos, numéricos y gráficos deberán estar siempre debidamente
justificados.
OPCIÓN A
|
PROBLEMA A.1. Dado el sistema de ecuaciones |
|
donde a es un parámetro real. Obtener razonadamente, escribiendo todos
los pasos del razonamiento utilizado:
a)
Los valores del parámetro a para los que el
sistema es compatible y determinado. (4 puntos)
b) Las soluciones del sistema cuando a = – 1. (3 puntos)
c)
El valor de a para que el sistema tenga una solución ( x, y, z ) que
verifique
x + y + z = 0. (3 puntos)
PROBLEMA A.2. Se tienen el plano
p: 2 x + y +2 z = 8 y el punto P = (10, 0, 10).
Obtener
razonadamente, escribiendo
todos los pasos del razonamiento utilizado:
a)
La distancia del punto
P al
plano π. (3 puntos)
b) El área del triángulo cuyos vértices son los puntos A, B y C,
obtenidos al hallar la intersección del
plano π con los ejes de coordenadas. (4 puntos)
c)
El volumen del tetraedro cuyos vértices son P, A,
B y C. (3 puntos)
|
PROBLEMA A.3.
Se da la función real h definida
por |
|
Obtener
razonadamente, escribiendo
todos los pasos del razonamiento utilizado:
|
a)
El dominio de
la función h. Los límites |
|
(1 + 2 puntos) |
b) La asíntota de la curva y = h(x). (4 puntos)
|
c)
La primitiva de
la función h (es decir, |
|
y el área de la superficie
encerrada |
entre las rectas y = 0,
x = 1, x = 5 y la
curva y = h(x). (4 puntos)
OPCIÓN B
|
PROBLEMA B.1.
Se dan las matrices |
|
Obtener
razonadamente, escribiendo
todos los pasos del razonamiento utilizado:
a)
Los valores de a para los que
la ecuación matricial A X = a X solo admite una solución. (4 puntos)
b) Todas las soluciones de la ecuación matricial A X
= 5 X. (3 puntos)
|
c)
Comprobar que |
|
es una solución de la
ecuación matricial A X = 2 X y, sin |
|
calcular
la matriz A100, obtener el valor de b tal que |
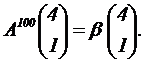
|
(2
puntos) |
|
PROBLEMA B.2.
Se dan en el espacio la recta |
|
y el
plano p: x + 2 y + 3 z = 6. |
Obtener
razonadamente, escribiendo
todos los pasos del razonamiento utilizado:
a)
La posición
relativa de la recta r
y el plano p en función de los parámetros reales a y b. (5 puntos)
b)
La distancia
entre la recta r y el plano p cuando a = 6
y b = 3. (4 puntos)
c)
La ecuación del
plano que pasa por ( 0,
0, 0 ) y que no corta al plano p. (2
puntos)
PROBLEMA B.3. un proyectil está unido al
punto (0, 2) por una cuerda elástica y tensa. El proyectil
recorre la curva y = 4 – x2 de extremos
( –
2, 0) y (2, 0).
Obtener
razonadamente, escribiendo
todos los pasos del razonamiento utilizado:
a)
La función de la
variable x que expresa la distancia
entre un punto cualquiera (x, 4 – x2)
de la curva y = 4 – x2 y el punto (0, 2). (2 puntos)
b)
Los puntos de la
curva y = 4 – x2 a mayor distancia absoluta del punto (0, 2)
para – 2 £ x £ 2. (2 puntos)
c)
Los puntos de la
curva y = 4 – x2 a menor distancia absoluta del punto (0, 2)
para – 2 £ x £ 2. (2 puntos)
d)
El área de la
superficie por la que se ha movido la cuerda elástica, es decir, el área
comprendida entre las curvas y = 4 –
x2 e y = 2 –
½x½ cuando – 2 £ x £ 2. (4 puntos)