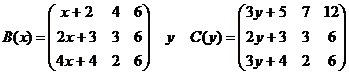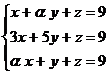Matemáticas II Junio 2007
Características de
la prueba.
Se elegirán TRES
bloques y se hará un problema de cada uno de ellos.
Cada problema se
puntuará de 0 a 3,3, según la puntuación máxima de cada apartado.
La suma de las
puntuaciones más 0,1 será la calificación de la prueba.
Cada estudiante
deberá disponer de una calculadora científica o gráfica para la realización del
examen. Se prohíbe su utilización indebida (para guardar fórmulas en memoria).
Se utilice o no la calculadora, los resultados analíticos o gráficos deben
estar debidamente justificados.
Bloque 1. ÁLGEBRA LINEAL.
|
Problema 1.1. Dadas las matrices |
|
a) Calcular el determinante de la matriz 3B(x)
y obtener el valor de x para el que dicho determinante
vale 162. (1,8 puntos).
b) Demostrar que la matriz C (y) no
tiene inversa para ningún valor real de y. (1,5 puntos).
|
Problema 1.2. Dado el sistema de ecuaciones lineales |
|
, se pide: |
a) Probar que es siempre compatible, obteniendo los
valores de 
para los que es
indeterminado.
(2 puntos).
b) Resolver el sistema anterior para 
. (1,3 puntos).
Bloque 2. GEOMETRÍA.
Problema 2.1. Dadas
las dos rectas r y s, que se cortan, de ecuaciones
|
|
, se pide calcular: |
a) El punto P de corte de las rectas r y
s. (1,1 puntos).
b) Un vector direccional de r y otro de s ,
(0,5 puntos), y el ángulo que forman las rectas r
y s en
el punto de corte P. (0,6 puntos).
c) La ecuación implícita a x + b
y + c z + d = 0 del plano π que
contiene a las rectas r y s (1,1 puntos).
Problema 2.2. Dados
el punto Q = (3, –1, 4) y la recta r de ecuación paramétrica
r: x = –2 + 3λ, y = –2λ, z =
1 + 4λ, se pide:
a) Hallar la distancia del punto Q a la recta r.
(1,1 puntos).
b) Justificar que la recta s que pasa por Q y
tiene a (1, −1, 1) como vector direccional no corta a r. (1,1
puntos).
c) Calcular la distancia
entre las rectas r y s. (1,1 puntos).
Bloque 3. ANÁLISIS.
Problema 3.1. Se
consideran las funciones reales f (x) = 12 x3 – 8 x2 + 9 x – 5 y
g(x) = 6 x2 – 7 x + 2. Se pide:
|
a) Determinar las ecuaciones de las asíntotas a la
gráfica de la función |
|
(1,6 puntos). |
|
b) Calcular la función |
|
que cumple H(1) = 1. (1,7 puntos). |
Problema 3.2. Se considera la función real f (x) = x3
+ a x2 + b x + c, donde a, b y c son parámetros
reales.
a) Averiguar los valores de
a y b para los que las rectas tangentes a la gráfica de f(x)
en los puntos de abscisas x = 2 y x = 4 son paralelas al eje OX. (2
puntos).
b) Con los valores de a y
b hallados anteriormente, obtener el valor de c para el que se
cumple que el punto de inflexión de la gráfica de f(x) está en el
eje OX. (1,3 puntos).
Bloque 4. RESOLUCIÓN DE PROBLEMAS.
|
Problema 4.1. Unos altos hornos producen al día x toneladas de acero de baja
calidad y |
|
toneladas |
de acero de alta calidad,
siendo 8 toneladas la producción máxima diaria de acero de baja calidad. Si el precio
de una tonelada de acero de baja calidad es 100 euros y el precio de una
tonelada de acero de alta calidad es 250 euros, demostrar que se deben producir
5 toneladas por día de acero de baja calidad para que el valor de venta de la
producción diaria sea máximo. (3,3 puntos).
Problema 4.2. Hallar las dimensiones del cartel de área máxima con forma de rectángulo que tiene dos vértices sujetos a una estructura rígida parabólica de ecuación y = 12 – x2 , y los otros dos vértices están situados sobre el eje OX . (3,3 puntos).