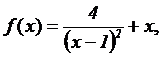Matemáticas II Junio
2025 (reserva)
BAREMO DEL EXAMEN: Cada
problema se puntuará hasta 2,5 puntos.
La calificación del
ejercicio será la suma de las calificaciones de cada problema.
Se permite el uso de
calculadoras siempre que no sean gráficas o programables, y que no puedan
realizar cálculos simbólicos ni almacenar texto o fórmulas en memoria. Se
utilice o no la calculadora, los resultados analíticos, numéricos y gráficos
deberán estar siempre debidamente justificados.
A partir de la
tercera falta de ortografía se deducirán -0,10 puntos hasta un máximo de un
punto.
Por errores en la
redacción, en la presentación, falta de coherencia, falta de cohesión,
incorrección léxica e incorrección gramatical se podrá deducir un máximo de
medio punto.
En las
respuestas se deben escribir todos los pasos del razonamiento utilizado.
PREGUNTA 1: PROBABILIDAD
Y ESTADÍSTICA (2,5 puntos)
Una firma automovilística fabrica tres modelos de coches: M1,
M2 y M3, y produce un 35% de vehículos en Estados Unidos, un 45% en China y un
20% en Alemania.
En la planta de Estados Unidos se
fabrican un 38% de vehículos del modelo M1, un 42% del M2 y un 20% del M3; en
la de China un 42% del M1, un 40% del M2 y un 18% del M3; y en la de Alemania
un 24% del M1, un 40% del M2 y un 36% del M3.
El control de calidad
ha detectado que en Estados Unidos un 3% de los coches presenta algún tipo de
defecto, en China un 4% y en Alemania un 1%.
1.1 (0.75 puntos) ¿Cuál es la
probabilidad de que un coche seleccionado al azar presente algún tipo de
defecto?
1.2 (0.75 puntos) Si un coche no presenta ningún defecto, ¿Cuál es la
probabilidad de que esté fabricado en Estados Unidos?
1.3 (1
punto) Dados 9 coches fabricados en
Alemania, calcular la probabilidad que al menos 3 sean
del modelo M2.
PREGUNTA 2: ÁLGEBRA (2,5 puntos)
Responda al apartado 2.1 o al apartado 2.2
2.1 Una
empresa de producción agrícola desarrolla fertilizantes que combinan tres
nutrientes esenciales: nitrógeno (N), fósforo (P) y potasio (K). Se representan
por x, y, z las cantidades en kilogramos a usar por lote de N, P, K,
respectivamente. Estas cantidades deben cumplir las siguientes restricciones:
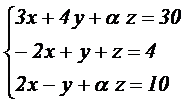
donde a es un
parámetro real.
2.1.1 (1.25 puntos) Discutir, en función del
parámetro a, el sistema de ecuaciones anterior.
2.1.2 (1.25 puntos) Obtener las cantidades x, y, z en el caso de que el sistema sea compatible.
___________________________________________________________________
2.2 Dadas las matrices
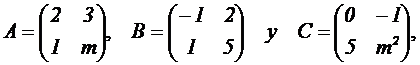
donde m es un
parámetro real, se pide:
2.2.1
(0.5 puntos) Calcular el
producto AB y la matriz traspuesta
de AB.
2.2.2
(0.75 puntos) En los casos en los que
A es invertible, calcular la inversa de A.
2.2.3 (0.75 puntos) Resolver la ecuación
matricial BX + A2 = C.
PREGUNTA 3: GEOMETRÍA (2,5 puntos)
Responda al apartado 3.1 o al apartado 3.2
|
3.1 Dados el plano
|
|
y la recta |
|
3.1.1 (0.75 puntos) Calcular la
distancia entre el punto (3, 1, – 2) y el plano p, en función del
parámetro real a.
3.1.2 (0.75 puntos) Para a =
4, calcular el ángulo que forma la recta
r con el plano
p.
|
3.1.3 (1 punto) Para a
= 3, calcular el punto simétrico del punto
|
|
respecto del |
|
plano p. |
|
|
___________________________________________________________________
|
3.2 Dada la recta |
|
que depende del parámetro real a, y la recta |
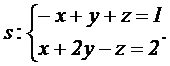
3.2.1 (1.25 puntos) Calcular el valor del parámetro real a para el que
r y s son perpendiculares.
3.2.2 (1.25
puntos) Suponiendo que a ¹ 0, obtener la recta paralela a s que pase por el punto de r cuya coordenada z vale 0.
PREGUNTA 4: ANÁLISIS (2,5 puntos)
Responda al apartado 4.1 o al apartado 4.2
4.1 Se considera un prisma
triangular de altura h cm, cuya base es un triángulo equilátero de lado x cm.
El prisma tiene área total (área que incluye el área de las caras laterales y
de las bases superior e inferior) igual a 10 cm2. Se pide:
4.1.1 (0.5 puntos) Expresar
el área total del prisma en función de x y h.
4.1.2
(1.5 puntos) Obtener los valores
de x y h que maximizan el volumen.
4.1.3 (0.5 puntos) Hallar dicho volumen.
___________________________________________________________________
|
4.2 Dada la función real de variable real |
|
se pide: |
4.2.1 (0.5 puntos) Calcular el dominio de
definición y las asíntotas de f.
4.2.2 (0.75 puntos) Indicar, si
existen, los extremos, y los intervalos de crecimiento y decrecimiento de f.
4.2.3 (0.5 puntos) Representar gráficamente la
función y = f(x).
4.2.4 (0.5 puntos) Calcular la integral
indefinida ò f(x) dx.
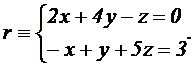
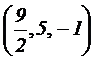
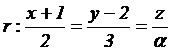 ,
,