Matemáticas II Septiembre 2006
Características de
la prueba.
Se elegirá el
EJERCICIO A o el EJERCICIO B, del que sólo se harán TRES de los problemas propuestos.
Cada problema se
puntuará de 0 a 3,3, según la puntuación máxima de cada apartado.
La suma de las
puntuaciones más 0,1 será la calificación de la prueba.
Cada estudiante
deberá disponer de una calculadora científica o gráfica para la realización del
examen. Se prohíbe su utilización indebida (para guardar fórmulas en memoria).
EJERCICIO A
PROBLEMA 1.
Dado el sistema de ecuaciones con un parámetro real λ
e incógnitas x, y, z,
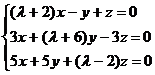
se pide:
a) Calcular para
qué valores de λ el sistema sólo admite la solución (x, y, z) = (0,
0, 0) (1 punto).
b) Para cada
valor de λ que hace indeterminado el sistema, obtener todas sus
soluciones (1,8 puntos).
c) Explicar la
posición relativa de los tres planos definidos por cada una de las ecuaciones
del sistema
·
La recta r intersección
de los planos de ecuaciones implícitas 2 x – 2 y – z = 9 y 4
x – y + z = 42.
·
Y la recta s
que pasa por los puntos (1,3,-4) y (3,-5,-2). Se pide:
a) Calcular las
ecuaciones paramétricas de la recta r (0,8 puntos) y de la recta s
(0,3 puntos).
b) Justificar que
las rectas r y s se cruzan (0,8 puntos).
c) Calcular un
vector direccional de la recta t, perpendicular común a las
rectas r y s, (0,4 puntos) y
PROBLEMA 3. Dadas
las funciones f (x) = x3
– 3 x + 8 y g(x) = − 3 x ,
se pide:
a) Calcular el
máximo absoluto de la función f (x) en el intervalo [ – 3 , 0 ]
(1 punto).
b) Calcular el
punto de corte de la curva y = f(x) y la recta y = g(x)
(1 punto).
c) Obtener el
área del recinto limitado por la curva y = f(x) y las rectas y = g(x), x = – 3 y x = 0.
PROBLEMA 4. Un incendio se extiende en forma circular
uniformemente. El radio del círculo quemado
a) Obtener el
área quemada en función del tiempo t transcurrido desde el comienzo del
incendio (1,3
b) Calcular la velocidad de crecimiento del área del círculo quemado en el instante en que el
radio
EJERCICIO B
|
PROBLEMA 1. A es una
matriz 3× 3 tal que |
|
Se pide:
a) Calcular el determinante de la matriz A3 (0,5
puntos) y la matriz inversa de A3 (1 punto).
b) Calcular la matriz fila X = (x, y, z)
que es solución de la ecuación matricial XA3 = BA2
, donde B es la
c) Calcular la matriz inversa de A (0,5 puntos).
PROBLEMA 2. En el espacio se consideran:
Ø
El plano π que pasa por los puntos (11, 1,
2), (5, 7, 5) y (7, –1, –2).
Ø
Y la recta r intersección de los planos
de ecuaciones implícitas x + y + z = 15 y 2x −
7y + 2z = 3 .
a) Calcular la ecuación paramétrica de r (0,6 puntos) y
la ecuación implícita del plano π (0,4 puntos).
b) Calcular el punto P intersección de r y π
(0,8 puntos) y el ángulo α que determinan r y π
(0,5 puntos).
c) Calcular los puntos M y N de la recta r cuya
distancia al plano π es igual a 3 u.l. (1 punto).
PROBLEMA 3.
a) Obtener la derivada de la función f(x) = ax +
b + sen x (0,5 puntos). Calcular a y b si
O = (0, 0) es un
|
b) Justificar que la función |
|
se anula en dos puntos
del intervalo [0,π] (0,5 puntos). |
c) Calcular esos dos puntos (0,5 puntos).
PROBLEMA 4.
Dos postes de 3m y 4
m se hallan clavados verticalmente en el suelo. Sus bases distan 5 m y,
en el segmento que las une, hay un punto P que dista x metros de
la base del poste más bajo. El extremo superior de cada poste se une con P mediante
un segmento rectilíneo de cable. Se pide:
a) Obtener la expresión f(x) de la longitud total de cable
utilizado en ambos segmentos (1,8 puntos).
b) Demostrar que esa longitud total de cable es mínima cuando son
iguales los valores absolutos de las