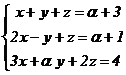Matemáticas II Septiembre 2008
Características de
la prueba.
Se elegirán TRES
bloques y se hará un problema de cada uno de ellos.
Cada problema se
puntuará de 0 a 3,3, según la puntuación máxima de cada apartado.
La suma de las
puntuaciones más 0,1 será la calificación de la prueba.
Cada estudiante
deberá disponer de una calculadora científica o gráfica para la realización del
examen. Se prohíbe su utilización indebida (para guardar fórmulas en memoria).
Se utilice o no la calculadora, los resultados analíticos o gráficos deben
estar debidamente justificados.
Bloque 1. ÁLGEBRA LINEAL.
|
Problema 1.1. Dada la matriz |
|
y el vector |
|
, se pide obtener razonadamente |
a) El vector X tal
que A X = 0X. (1,1
puntos).
b)
Todos los vectores X tales
que A X = 3X. (1,1
puntos).
c) Todos los vectores X tales que
A X = 2X. (1,1 puntos).
|
Problema 1.2. Dado el sistema de ecuaciones lineales |
|
, se pide: |
a) Probar que es compatible
para todo valor de α. (1,3 puntos).
b) Obtener razonadamente el valor de α para el que el sistema es indeterminado. (1
punto).
c) Resolver el sistema cuando
α = 0, escribiendo los cálculos
necesarios para ello. (1 punto).
Bloque 2. GEOMETRÍA.
Problema 2.1. Dados
los planos π1: x + y + z = 3
y π2: x + y – α z = 0, se pide calcular
razonadamente:
a) El valor de α para que los planos π1 y π2 sean perpendiculares
y, para este valor de α, obtener las ecuaciones paramétricas de la recta
intersección de estos dos planos. (1,5 puntos).
b) El valor de α
para que los planos π1 y π2 sean paralelos y,
para este valor de α, obtener la distancia entre los dos planos π1 y π2 . (1,8 puntos).
Problema 2.2. Dados
el punto O = ( 0 , 0 , 0 ) y el
plano π: x + y + z = 6, se pide calcular razonadamente:
a) La ecuación de la recta r que pasa por O y
es perpendicular al plano π. (1,1 puntos).
b) Las coordenadas del punto simétrico de O respecto del plano π. (1,1 puntos).
c) La ecuación del plano que
contiene al eje X y a la recta r. (1,1 puntos).
Bloque 3. ANÁLISIS.
Problema 3.1. Dada
la función f(t) = a t + b (con a
y b constantes reales), se define 
. Se pide obtener razonadamente:
|
a) La
integral |
|
(1,5 puntos). |
b)
La expresión de la derivada F´(x) de la función
F(x). (0,5 puntos).
c)
La relación entre los valores a
y b para la que se verifica: F´´(0) = 0. (1,3 puntos).
Problema 3.2. Para cada número real
positivo α, se considera la función g(x) = x2 + α. Se
pide calcular razonadamente:
a) El área de la región del
plano limitada por el eje X, el eje Y, la recta 
y la curva y = g(x).
(2 puntos).
b) El valor de α para el que la curva y = x2
+ α divide al rectángulo de
vértices (0,0), (
,0), (, 6 + α), (0, 6 + α) en dos regiones de igual área.
(1,3 puntos).
Bloque 4. RESOLUCIÓN DE PROBLEMAS.
Problema 4.1. Un móvil se mueve con velocidad constante de 2m/s, en
el primer cuadrante, sobre la recta x = 1, partiendo del punto M = (1,0) situado a 1 m del origen. Se pide obtener
razonadamente:
a)
Las coordenadas del punto M(t) donde está situado el móvil después de t
segundos. (1 punto).
b)
La función m(t) igual a la pendiente de la recta que
pasa por el punto O = (0,0) y por el
punto M(t). (1,3 puntos).
c)
La derivada de la
función m(t). (1 punto).
Problema 4.2. En un terreno con forma de semicírculo de radio 
metros, se dibuja un
rectángulo que tiene dos vértices sobre la semicircunferencia del perímetro del
terreno. Los otros dos vértices del rectángulo están sobre el segmento
rectilíneo de dicho perímetro y distan x metros. Obtener razonadamente:
a)
El área del rectángulo en función de
x. (1,3 puntos).
b)
El valor de x para el que es máxima el área del rectángulo.
(2 puntos).